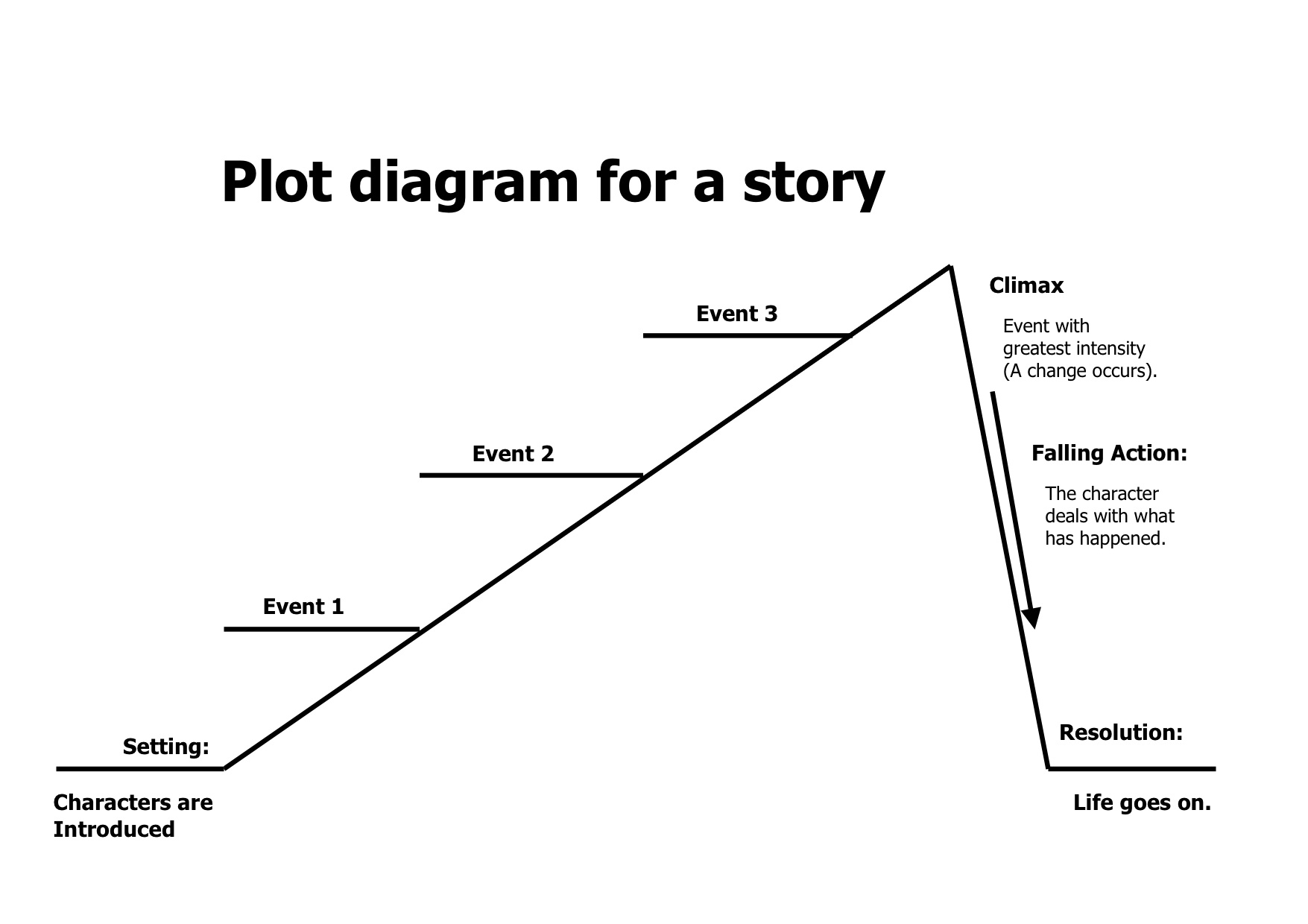
5 Plots In Order
Recall that the second condition — the 'I' condition — of the linear regression model is that the error terms are independent. In this section, we learn how to use a 'residuals vs. order plot' as a way of detecting a particular form of non-independence of the error terms, namely serial correlation. If the data are obtained in a time (or space) sequence, a residuals vs. order plot helps to see if there is any correlation between the error terms that are near each other in the sequence.
- In essence, the ordered data plot may be viewed as a scatter plot of the ordered data versus a single n-treatment consolidation factor. Motivation To determine the best setting, an obvious place to start is the best response value.
- During the summer, Harry Potter and his cousin Dudley are attacked by Dementors.Forced to use magic to fend them off, Harry is expelled from Hogwarts, but his expulsion is postponed pending a hearing at the Ministry of Magic.Harry is whisked off to Number 12, Grimmauld Place, the childhood home of Sirius Black, by a group of wizards belonging to the Order of the Phoenix.
The plot is only appropriate if you know the order in which the data were collected! Highlight this, underline this, circle this, ..., er, on second thought, don't do that if you are reading it on a computer screen. Do whatever it takes to remember it though — it is a very common mistake made by people new to regression analysis.
So, what is this residuals vs. order plot all about? As its name suggests, it is a scatter plot with residuals on the y axis and the order in which the data were collected on the x axis. Here's an example of a well-behaved residuals vs. order plot:
The residuals bounce randomly around the residual = 0 line as we would hope so. In general, residuals exhibiting normal random noise around the residual = 0 line suggest that there is no serial correlation.
Free $25 off any order of $50 or more TODAY! 0 Item(s) $0.00 0 $0.00 Search Item Number or Keyword. Asparagus; Beans - Bush. Created using PowToon - Free sign up at. Make your own animated videos and animated presentations for free. PowToon is a free.
Let's take a look at examples of the different kinds of residuals vs. order plots we can obtain and learn what each tells us.
A time trend
A residuals vs. order plot that exhibits (positive) trend as the following plot does:
suggests that some of the variation in the response is due to time. Therefore, it might be a good idea to add the predictor 'time' to the model. That is, you interpret this plot just as you would interpret any other residual vs. predictor plot. It's just that here your predictor is 'time.'
Positive serial correlation
A residuals vs. order plot that looks like the following plot:
suggests that there is 'positive serial correlation' among the error terms. That is, positive serial correlation exists when residuals tend to be followed, in time, by residuals of the same sign and about the same magnitude. The plot suggests that the assumption of independent error terms is violated.
Here is another less obvious example of a data set exhibiting positive serial correlation:
Can you see a cyclical trend -- up and then down, up and down, and up again? If not, click on the 'Draw trend!' icon. Certainly, the positive serial correlation in the error terms is not as obvious here as in the previous example. These two examples taken together are a nice illustration of 'the severity of the consequences is related to the severity of the violation.' The violation in the previous example is much more severe than in this example. Therefore, we should expect that the consequences of using a regression model in the previous example would be much greater than using one in this example. In either case, you would be advised to move out of the realm of regression analysis and into that of 'time series modeling.'
Negative serial correlation
A residuals vs. order plot that looks like the following plot:
suggests that there is 'negative serial correlation' among the error terms. Negative serial correlation exists when residuals of one sign tend to be followed, in time, by residuals of the opposite sign. What? Can't you see it? If you connect the dots in order from left to right, you should be able to see the pattern. If you can't see it, click on the 'Draw trend!' icon:
Negative, positive, negative, positive, negative, positve, and so on. The plot suggests that the assumption of independent error terms is violated. If you obtain a residuals vs. order plot that looks like this, you would again be advised to move out of the realm of regression analysis and into that of 'time series modeling.'
- Control Systems Tutorial
- Control Systems Useful Resources
- Selected Reading
The Bode plot or the Bode diagram consists of two plots −
- Magnitude plot
- Phase plot
In both the plots, x-axis represents angular frequency (logarithmic scale). Whereas, yaxis represents the magnitude (linear scale) of open loop transfer function in the magnitude plot and the phase angle (linear scale) of the open loop transfer function in the phase plot.
The magnitude of the open loop transfer function in dB is -
$$M=20: log G(jomega)H(jomega) $$
The phase angle of the open loop transfer function in degrees is -
$$phi=angle G(jomega)H(jomega)$$
Note − The base of logarithm is 10.
Basic of Bode Plots
The following table shows the slope, magnitude and the phase angle values of the terms present in the open loop transfer function. This data is useful while drawing the Bode plots.
| Type of term | G(jω)H(jω) | Slope(dB/dec) | Magnitude (dB) | Phase angle(degrees) |
|---|---|---|---|---|
Constant | $K$ | $0$ | $20 log K$ | $0$ |
Zero at origin | $jomega$ | $20$ | $20 log omega$ | $90$ |
‘n’ zeros at origin | $(jomega)^n$ | $20: n$ | $20: n log omega$ | $90: n$ |
Pole at origin | $frac{1}{jomega}$ | $-20$ | $-20 log omega$ | $-90 : or : 270$ |
‘n’ poles at origin | $frac{1}{(jomega)^n}$ | $-20: n$ | $-20 : n log omega$ | $-90 : n : or : 270 : n$ |
Simple zero | $1+jomega r$ | $20$ | $0: for: omega < frac{1}{r}$ $20: log omega r: for : omega > frac{1}{r}$ | $0 : for : omega < frac{1}{r}$ $90 : for : omega > frac{1}{r}$ |
Simple pole | $frac{1}{1+jomega r}$ | $-20$ | $0: for: omega < frac{1}{r}$ $-20: log omega r: for: omega > frac{1}{r}$ | $0 : for : omega < frac{1}{r}$ $-90: or : 270 : for: omega > frac{1}{r}$ |
Second order derivative term | $omega_n^2left ( 1-frac{omega^2}{omega_n^2}+frac{2jdeltaomega}{omega_n} right )$ | $40$ | $40: log: omega_n: for : omega < omega_n$ $20: log:(2deltaomega_n^2): for : omega=omega_n$ $40 : log : omega:for :omega > omega_n$ | $0 : for : omega < omega_n$ $90 : for : omega = omega_n$ $180 : for : omega > omega_n$ |
Second order integral term | $frac{1}{omega_n^2left ( 1-frac{omega^2}{omega_n^2}+frac{2jdeltaomega}{omega_n} right )}$ | $-40$ | $-40: log: omega_n: for : omega < omega_n$ $-20: log:(2deltaomega_n^2): for : omega=omega_n$ $-40 : log : omega:for :omega > omega_n$ | $-0 : for : omega < omega_n$ $-90 : for : omega = omega_n$ $-180 : for : omega > omega_n$ |
Consider the open loop transfer function $G(s)H(s) = K$.
Magnitude $M = 20: log K$ dB
Phase angle $phi = 0$ degrees
If $K = 1$, then magnitude is 0 dB.
If $K > 1$, then magnitude will be positive.
If $K < 1$, then magnitude will be negative.
The following figure shows the corresponding Bode plot.
The magnitude plot is a horizontal line, which is independent of frequency. The 0 dB line itself is the magnitude plot when the value of K is one. For the positive values of K, the horizontal line will shift $20 :log K$ dB above the 0 dB line. For the negative values of K, the horizontal line will shift $20: log K$ dB below the 0 dB line. The Zero degrees line itself is the phase plot for all the positive values of K.
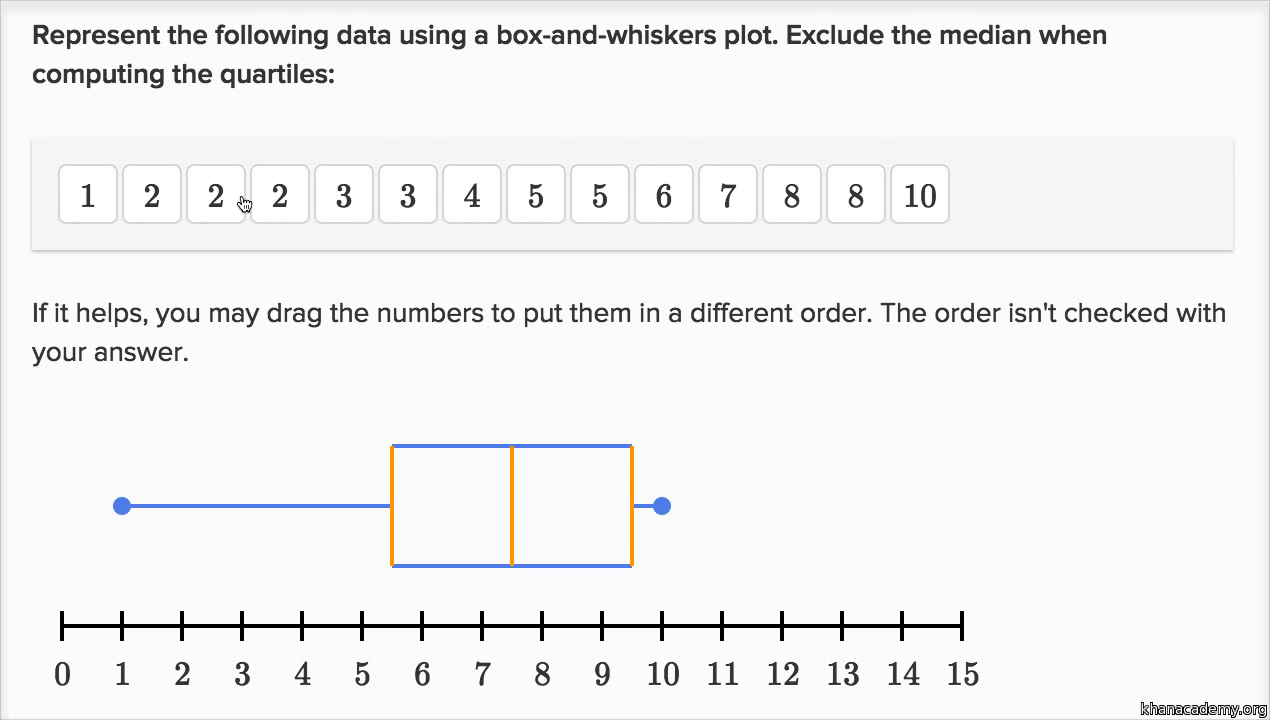
5 Plots In Order Worksheets
Consider the open loop transfer function $G(s)H(s) = s$.
Magnitude $M = 20 log omega$ dB
Phase angle $phi = 90^0$
At $omega = 0.1$ rad/sec, the magnitude is -20 dB.
5 Plots In Order Worksheet
At $omega = 1$ rad/sec, the magnitude is 0 dB.
At $omega = 10$ rad/sec, the magnitude is 20 dB.
The following figure shows the corresponding Bode plot.
The magnitude plot is a line, which is having a slope of 20 dB/dec. This line started at $omega = 0.1$ rad/sec having a magnitude of -20 dB and it continues on the same slope. It is touching 0 dB line at $omega = 1$ rad/sec. In this case, the phase plot is 900 line.
Consider the open loop transfer function $G(s)H(s) = 1 + stau$.
Magnitude $M = 20: log sqrt{1 + omega^2tau^2}$ dB
Phase angle $phi = tan^{-1}omegatau$ degrees
For $ω < frac{1}{tau}$ , the magnitude is 0 dB and phase angle is 0 degrees.
For $omega > frac{1}{tau}$ , the magnitude is $20: log omegatau$ dB and phase angle is 900.
The following figure shows the corresponding Bode plot.
The magnitude plot is having magnitude of 0 dB upto $omega=frac{1}{tau}$ rad/sec. From $omega = frac{1}{tau}$ rad/sec, it is having a slope of 20 dB/dec. In this case, the phase plot is having phase angle of 0 degrees up to $omega = frac{1}{tau}$ rad/sec and from here, it is having phase angle of 900. This Bode plot is called the asymptotic Bode plot.
As the magnitude and the phase plots are represented with straight lines, the Exact Bode plots resemble the asymptotic Bode plots. The only difference is that the Exact Bode plots will have simple curves instead of straight lines.
Similarly, you can draw the Bode plots for other terms of the open loop transfer function which are given in the table.